descomp

r e s e a r c h

C o n s t r u c t i n g   D e s i g n   C o n c e p t s :   A Computational Approach to the Synthesis of Architectural Form Kotsopoulos S, Ph.D. Dissertation, Massachusetts Institute of Technology, 2005

II.    Shape Computation Theory         1.  Introduction       2.  Computational Theory       3.  Computational Design Theory       4.  Shape Computation           4.1. SHAPE CALCULUS                                                                                                                                       A     B     C       A shape calculus is a computational framework where shapes of 0, 1, 2 and 3 dimensions are used in       calculations that take place in 0, 1, 2 or 3 dimensions. Shape algebras offer a formal account of the spatial          properties of shapes and the ways in which they interact.       The construction of shape algebras by Stiny (1991) follows the empirical observation that zero dimensional points       interact differently from shapes of dimension greater than zero. Points remain always undivided and discreet.       Higher dimensional elements like lines, planes or solids can be divided and embedded on one another in infinite       ways. This has some interesting computational and visual consequences. Shapes made out of lines, planes or       solids can be decomposed in infinite sets of lines, planes or solids respectively. This allows shapes that look the       same to be described by different sets of 0-dimensional points. To treat this ambiguity in the description of       shapes Stiny (1975) proposed to describe shapes of higher than zero dimensions by their maximal elements.       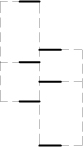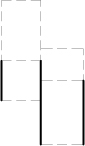A shape made out of lines,

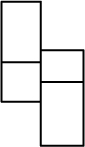
can be described uniquely by a set containing nine maximal lines. The maximal elements of a shape are the larger       parts that describe the shape without having common parts. In the example the maximal elements are three       vertical, and six horizontal lines.

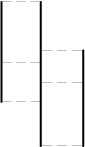
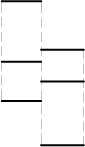
But the initial shape can also be analyzed in alternative ways. The following option contains six vertical lines, and       twelve horizontal lines.

Similarly, the next arrangement made out of solids, representing walls,

can be analyzed in a set containing nine solid elements: three vertical and six in width horizontal.

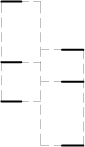
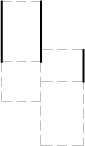
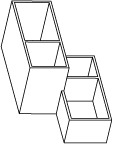
And, the initial solid can be decomposed in alternative ways to provide different sets of parts. For example,  six      vertical, and twelve horizontal solid parts.