a  c  a  d  e  m  i  c

r e s e a r c h

C o n s t r u c t i n g   D e s i g n   C o n c e p t s :   A Computational Approach to the Synthesis of Architectural Form Kotsopoulos S, Ph.D. Dissertation, Massachusetts Institute of Technology, 2005

II.     Shape Computation Theory                                                                      4.2. SHAPE GRAMMAR                                  4.2 1.  What is a shape rule ?      A shape rule is a production of the form a  --> b,  between two shapes  a, b . The shapes need to belong to some      shape algebra Uij within which shape operations can be executed, and the transformations together with the      embedding relationship  can be used. A shape rule is a computational device that allows the  two shapes a, b to be      placed together (com-posed)  in some desired way.          The  next  example,  shows how two shapes are put  together to form a particular relationship. The shapes a, b of      the example are made out of lines. They belong to the algebra U12 , which contains lines manipulated on the plane.      A shape rule of the general form a --> b applies to some initial shape C like the next, under some transformation t.

C

Suppose that  the next spatial relationship is a desired one:

The initial and the concluding states a and  b can be connected by a shape rule, in the following way,

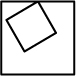
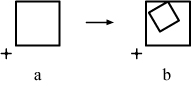
The  above rule treats the desired relationship in a particular way: As  a relationship between two squares.           The  rule a --> b applies on a shape C in two steps. First, some transformation t (in this case scaling) is used with     the part relation  < to "match" some part of the given shape C to the shape a, which appears on the left side.

t ( a )  <  C

Second, if there is a "match" between t ( a ) and C, the operation of shape subtraction ( - ) is used to subtract t ( a )     from C. And, the operation of shape addition (+) is used to add the same transformation t of the shape b, to C.  The     shape b is the one that we see on the right side of the shape rule.

t ( a )  <  C                                                                 [ C - t (a) ]                                                              [ C - t (a) ]  + t (b)

When we apply a  rule  a --> b on some shape C, a new shape C' is produced.

C'

The new shape C' is produced from C according to the relationship:                                                                                         C'  =    [ C - t (a) ]  + t (b)